2010 October 16 / |j|d|a|v|i|s|@|c|a|r|l|e|t|o|n|.|e|d|u
Carleton College CS 201, Prof. Joshua R. Davis
The purpose of this short assignment is to understand the AVL tree. Recall that an AVL tree is approximately balanced, in that at each node the height of the left and right subtrees differ by at most one. Maintaining this level of balance keeps the height of the tree small relative to the number of nodes, and hence keeps all of our binary search tree operations fast.
Because height is used so frequently in an AVL tree, it makes sense for each node to store its height (meaning the height of the tree hanging off it), rather than recompute the height each time it's needed. Thus an AVL tree node stores a key, a value, and a height, whereas an ordinary binary search tree node stores just a key and a value. We could make our AVLTreeNode class a subclass of BinarySearchTreeNode, but the methods (specifically put and delete) are sufficiently different that we'll implement AVLTreeNode as a new subclass of BinaryTreeNode.
In fact, I've already written most of the implementation for you, by modifying BinarySearchTreeNode's code to perform balancing operations recursively after each put and delete operation. You are required to write the AVL balancing operation; then AVLTreeNode is finished. Then you are required to implement IntDictionary and Dictionary atop AVLTreeNode.
You may complete this assignment with one partner, although it's not the kind of work that's easily divided up. It is due Wednesday at 11:59 PM.
AVLTreeNode
Download the file avltreenode.py to your computer. Most of it has been written for you already. There are various methods for getting and setting height. The get method is identical to BinarySearchTreeNode's. The put and delete methods have been modified (from BinarySearchTreeNode's versions) to rebalance the tree, by calling the balance method. So they're done. But right now balance does very little; it just updates the height, without actually balancing anything. Your job is to implement balance for real.
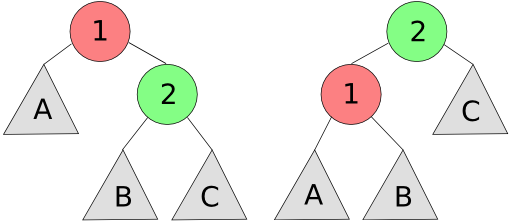
Remember from class that we use two fundamental "rotation" operations to balance a tree. In the illustration below, individual nodes are drawn as circles, and subtrees are drawn as triangles. In the tree on the left, a left rotation at node 1 produces the tree on the right. That is, the left rotation shifts node 2 up to the root, shifts node 1 into node 2's left subtree, and reconfigures all other parts of the tree in the only way possible, that maintains the binary search tree property. The right rotation is simply the inverse operation; that is, in the tree on the right, a right rotation at node 2 produces the tree on the left.

Now, a put or delete operation on an AVL tree node may temporarily put a tree node out of AVL balance. There are four possible ways in which a node can be out of balance, called RR, LL, RL, and LL. The RR case is illustrated on the left side of the figure below. It occurs when the height of the right subtree of node 1 exceeds the height of the left subtree of node 1 by more than one, and the right subtree of node 2 is at least as tall as the left subtree of node 2. You can rebalance the tree by performing a left rotation on node 1; the result is shown on the right side of the figure below.
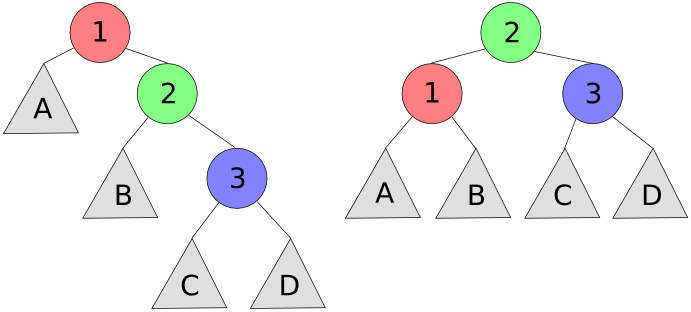
The LL case is symmetric to the RR case. Draw it out for yourself. You can rebalance the tree by performing a right rotation on the root.
The RL case is illustrated on the left side of the figure below. It occurs when the height of the right subtree of node 1 exceeds the height of the left subtree of node 1 by more than one (as in the RR case), but the left subtree of node 3 is taller than the right subtree of node 3 (unlike the RR case). To handle this case, you perform a right rotation on node 3. The result is shown on the right side of the figure. It's not balanced yet, but it's in the RR configuration, which you can balance using a left rotation. So rebalancing the RL case requires a total of two rotations.
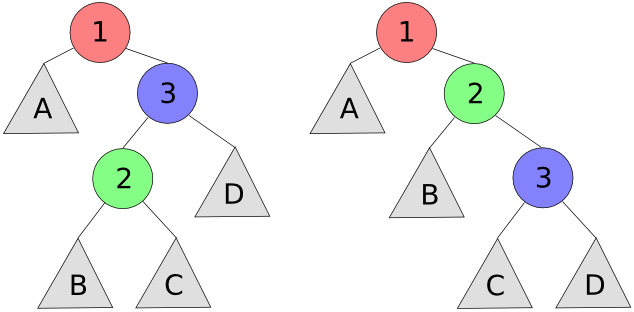
The LR case is symmetric to the RL case. Draw it out for yourself. You can rebalance the tree by performing a left rotation followed by a right rotation.
Your job is to implement balance by recognizing these four cases and performing rotations. You might want to write helper methods for performing the rotations; it's up to you. You do not need to perform any recursion; you just need to balance at a single node, under the assumption that its subtrees have already been balanced.
Download the file intdictionary_bstn.py from the course web site. Rename it to intdictionary_avltn.py. Edit it to use AVLTreeNode instead of BinarySearchTreeNode. This requires a few small changes, because the interface of the AVLTreeNode class is not identical to the interface for the BinarySearchTreeNode class. The integer dictionary class should still be IntDictionary, and its methods should work identically to our old IntDictionary's — only more quickly.
Make a copy of your file dictionary_bstn.py from the previous assignment. It uses the integer dictionary based on BinarySearchTreeNode, right? But now we know that unbalanced binary search trees are for losers. Rename the file to dictionary_avltn.py, and edit it to use the integer dictionary based on AVLTreeNode. This should require very few changes. Again, the class should still be called Dictionary, and its methods should work identically to our old Dictionary's, but more quickly.
Moral: The user of a class, method, or function just needs to know what it does (the interface), not how it does it (the implementation). If we're supplying a Dictionary class to our users, then we should be able to change its implementation, as long as we don't change its interface. When the users discover that our new Dictionary is faster than our old one, but doesn't break any of their software, perhaps they will give us a soft, chewy cookie.
After testing them thoroughly, submit your three files avltreenode.py, intdictionary_avltn.py, and dictionary_avltn.py electronically as usual. They will be graded according to these criteria:
AVLTreeNode works, including correct balancing behavior (3 points).
IntDictionary and Dictionary atop AVLTreeNode work (3 points).