2009 February 13 / jj|d|a|v|i|s|@|c|a|r|l|e|t|o|n|.|e|d|u

Senior Seminar: Manifolds

Carleton College Math 395, Winter 2009, Prof. Joshua R. Davis

Introduction

The first goal of this course is Stokes' theorem, which generalizes the fundamental theorem of calculus to manifolds of arbitrary dimension. Applications of Stokes' theorem can be found throughout mathematics and physics; I have even seen the theorem in geology papers. But what is truly impressive about this theorem is its elegance. The proof is not difficult, and the end result is the short but powerful formula

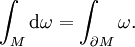
Of course, such a formula in isolation is meaningless; I have not stated the hypotheses or defined any of the terms, because the definitions are subtle and abstract. Indeed, Stokes' theorem is a good first example of the "big machinery" approach to mathematics, in which definitions are difficult, proofs are easy, and results seem natural and simple. Our primary text for this material is Calculus on Manifolds by Michael Spivak.

After we learn Stokes' theorem, we will investigate other topics as the students desire: more concepts in differential topology, applications to physics, connections to complex analysis or algebra, etc. If the students' interests vary greatly, then we may split into individual or group projects.

Logistics

We meet in CMC 328 during period 5A (MW 1:50PM-3:00PM, F 2:20PM-3:20PM). Here's how you get in contact with me:

Dr. Joshua R. Davis (call me Josh if you like)
E-mail: jj|d|a|v|i|s|@|c|a|r|l|e|t|o|n|.|e|d|u
Office: CMC 327, x4482
Office hours: Sun 12-1, Tue 10-11, Wed 3-4, and Thu 3-4. You can also make an appointment; simply pick a free time from my weekly schedule and e-mail me. You can also talk to me after class.

This course is unique, and there are few students, so the usual statistical approach to grading is inappropriate. Students will be graded individually, based on the following criteria.

• On a rotating basis, the students will present material to the group for up to half of each class meeting.
• We will do some of the book's problems, either writing them up or presenting them in class.
• There are no exams.

Schedule

Please complete the Introductory Survey by Monday 11:59 PM.

Date	Day	Reading	Topic	Problems
M 1/05	01	forward, preface	introduction
W 1/07	02	1.1, 1.2	Euclidean space
F 1/09	03	1.3, 2.1	differentiability	prove Chain Rule nicely
M 1/12	04	2.2	chain rule	1.10, 2.1
W 1/14	05	2.3	partial derivatives
F 1/16	06	2.4	continuous differentiability
M 1/19	07	2.5	inverse function theorem
W 1/21	08	2.6	manifolds
F 1/23	09	3.1, 3.2	integration
M 1/26	10	3.4	Fubini's theorem	3.28, 3.35
W 1/28	11	3.3, 3.5	integrability
F 1/30	12	3.6	partition of unity
M 2/02	13	3.6	change of variables	3.28, 3.35
W 2/04	14	3.6
F 2/06	15	4.1	Sard's theorem
M 2/09	--	MIDTERM BREAK
W 2/11	16	4.1	multilinear algebra
F 2/13	17	4.1		4.3, 4.5, 4.6, 4.11
M 2/09	--	4.1
W 2/11	16	4.1
F 2/13	17	4.1
M 2/16	18	4.2	differential forms
W 2/18	19	4.2
F 2/20	20	4.2	homework
M 2/23	21	4.2	exterior differentiation
W 2/25	22	4.2	Poincare lemma
F 2/27	23	4.3	singular n-cubes
M 3/02	24	4.4	fundamental theorem
W 3/04	25	5.1, 5.2	manifolds
F 3/06	26	5.3	Stokes' theorem
M 3/02	27	5.4, 5.5	classical Stokes' theorems
W 3/04	28		de Rham cohomology